The General Künneth Formula
The General Künneth Formula
Künneth formulae help us relate the (co)homology of a product space to the (co)homology of the factors. Recall that in Theorem 3.15 of Hatcher, we showed that if one of the factors has finitely generated, free cohomology groups, then \[H^*(X \times Y;R) \cong H^*(X;R) \otimes H^*(Y;R)\] In particular, we used the fact that finitely-generated free modules are flat (meaning that tensoring with them preserves exact sequences). In the general case, our modules will not necessarily be flat. The left derived functor corresponding to taking tensor products is called $\Tor$, and it will help us derive a general Künneth formula. It turns out that it is more natural to derive this general Künneth formula for homology, so we will do so.
Algebraic Preliminaries
Defining the Künneth formula for homology will be easier if we begin by building up some algebraic machinery.
The Tensor Product of Chain Complexes
Suppose that we have two chain complexes $(X_\bullet, \partial^X_\bullet)$ and $(Y_\bullet, \partial^Y_\bullet)$. We have seen earlier that we can define a direct sum of these complexes using the simple definition that $(X \oplus Y)_i = X_i \oplus Y_i$ and $\partial^{X \oplus Y}_i = \partial^X_i \oplus \partial^Y_i$. It would be natural to try to define the tensor product of the chain complexes analogously, but that turns out to be poorly-behaved.
A better definition is $(X \otimes Y)_k = \bigoplus_{i+j=k} X_i \otimes Y_j$ with boundary maps $\partial^{X \otimes Y}_k (x \otimes y) = \partial^X_ix \otimes y + (-1)^i x \otimes \partial^Y_j y$ for $x \in X_i, y \in Y_j, i+j=k$. This can be seen as the total complex of a bicomplex whose modules are given by $X_i \otimes Y_j$.
One indication that this is a good definition for the tensor product of chain complexes is that the category of chain complexes of $R$-modules has an internal hom, given by the following chain complex \[\Big(\Hom(X,Y)\Big)_k = \prod_i \Hom_R(X_i, Y_{i+k})\] \[\left(\partial^{\Hom(X,Y)}_kf\right)(v) = \partial^Y_{}(f(v)) - (-1)^k f(\partial^X_{}(v))\] It turns out that, as one might expect, the tensor product of chain complexes is adjoint to the internal hom in the sence that for chain complexes $A,B,C$, we have a natural isomorphism \[\Hom(A \otimes B,C) \cong \Hom(A, \Hom(B,C))\]
The Algebraic Künneth Formula
There is a nice relationship between the homology groups of chain complexes and the homology groups of their tensor product. Hatcher calls this the algebraic version of the Künneth formula.
First, we will consider the special case where the boundary maps in $C$ are all zero. This means that $H_i(C) = C_i$. Since the boundary maps are zero, the boundary map in the tensor product complex simplifies to $\partial(c \otimes c') = (-1)^{|c|} c \otimes \partial c'$. Thus, the complex $C \otimes_R$ is simply the direct sum of the complexes $C_i \otimes_R C'$, and each of these complexes is a direct sum of copies of $C'$ because $C_i$ is free. So \[H_n(C_i \otimes_R C') \cong C_i \otimes_R H_{n-i}(C') = H_i(C) \otimes_R H_{n-i}(C')\] Taking a direct sum over $i$ gives us an isomorphism \[H_n(C \otimes_R C') \cong \bigoplus_i H_i(C) \otimes_R H_{n-i}(C')\] and this is precisely what we needed to prove. The $\Tor$ terms in the theorem statement are 0 since in this case $H_i(C) = C_i$ is free.
Now, we will consider the general case. Let $Z_i, B_i \subseteq C_i$ denote the cycles and boundaries in $C_i$ respectively (i.e. the kernel and image of the boundary maps). We can construct chain complexes $Z$ and $B$ with trivial boundary maps, and these yield a short exact sequence of chain complexes $0 \to Z \to C \to B \to 0$. This is composed of the short exact sequences $0 \to Z_i \to C_i \xrightarrow{\partial} B_{i-1} \to 0$. Note that these short exact sequences split since $B_{i-1}$ is free (since it is a submodule of the free module $C_{i-1}$). Because these short exact sequences split, tensoring with $C'$ gives us another short exact sequence, so tensoring our short exact sequence of chain complexes gives another short exact sequence of chain complexes. This gives us a long exact sequence of homology groups
\[\cdots \to H_n(Z \otimes_R C') \to H_n(C \otimes_R C') \to H_{n-1}(B \otimes_R C') \to H_{n-1}(Z \otimes_R C') \to \cdots\]The homology group $H_{n-1}(B \otimes_R C')$ is shifted down a degree from what one might expect because $B_{i-1}$ appears in the short exact sequence above instead of $B_i$. It turns out that the boundary map $H_{n-1}(B \otimes_R C') \to H_{n-1}(Z \otimes_R C')$ is induced by the inclusion $B_i \subseteq Z_i\;\forall i$.
Since $B$ and $Z$ are chain complexes whose boundary maps are all 0, we can apply the computation we did above to turn $H_n(Z \otimes_R C')$ into $\bigoplus_i Z_i \otimes_R H_{n-i}(C')$ and the same for $B$. This gives us a long exact sequence \[\cdots \xrightarrow{i_n} \bigoplus_i Z_i \otimes_R H_{n-i}(C') \to H_n(C \otimes_R C') \to \bigoplus_i B_i \otimes_R H_{n-i-1}(C') \xrightarrow{i_{n-1}} \cdots\] We can split this long exact sequence up into many short exact sequences. In particular, we find short exact sequences \[0 \to \Coker i_n \to H_n(C \otimes_R C') \to \Ker i_{n-1} \to 0\] By definition, $\Coker i_n = \left(\bigoplus_j Z_j \otimes_R H_{n-j}(C')\right)/\Im i_n$. We can view $i_n$ as the map which applies $i:B \inj Z$ on the first tensor factor, and the identity on the second tensor factor. Since taking a tensor product with a fixed module is a right exact functor, we conclude that \[\left(\bigoplus_j Z_j \otimes_R H_{n-j}(C')\right)/\Im \bigoplus_j (i \otimes_R 1) \cong \bigoplus_j \left(Z_j / \Im i\right) \otimes_R H_{n-j}(C') \cong \bigoplus_j H_j(C) \otimes_R H_{n-j}(C')\] Now, we only have to show that $\Ker i_{n-1}$ is $\bigoplus_i \Tor_R(H_i(C), H_{n-i}(C'))$.
$\Tor$ is the left derived functor corresponding to taking tensor products. So taking the short exact sequence $0 \to B_i \to Z_i \to H_i(C) \to 0$ and tensoring with $H_{n-i}(C')$ yields a long exact sequence
Since $Z_i$ is a submodule of a free module, it is free. So $\Tor^1_R(Z_i, H_{n-i}(C'))$ is 0. Thus, we have an exact sequence \[0 \to \Tor_R(H_i(C), H_{n-i}(C')) \to B_i \otimes_R H_{n-i}(C') \to Z_i \otimes_R H_{n-i}(C')\] The rightmost map in this sequence is again induced by the inclusion $B_i \inj Z_i$. So after summing over $i$, we see that $\Ker i_n$ is precisely $\bigoplus_i \Tor_R(H_i(C), H_{n-i}(C'))$.Naturality essentially follows because all of the exact sequences and operations on them that we considered are natural.
We will only show the splitting in the case that $C$ and $C'$ are both free, although it is true that the sequence splits in the general case as well. We will show that the short exact sequence is split by constructing a homomorphism $H_n(C \otimes_R C') \to \bigoplus_i(H_i(C) \otimes_R H_{n-i}(C'))$. We observed earlier that the sequence $0 \to Z_i \to C_i \to B_{i-1} \to 0$ splits. Thus, we have a splitting map $s:C_i \to Z_i$. Using this splitting map, we can lift the quotient $Z_i \to H_i(C)$ to a map $C_i \to H_i(C)$. Similarly, using the assumption that $C'$ is free, we can construct maps $C_j' \to H_j(C')$. Now, we can construct chain complexes $H(C), H(C')$ whose modules are $H_i(C)$ and $H_j(C')$ respectively, and whose boundary maps are all trivial. Then the lifts of the quotient maps that we constructed give us chain maps $C \to H(C), C' \to H(C')$. Taking the tensor product of these chain maps gives us a chain map $C \otimes_R C' \to H(C) \otimes_R H(C')$. This induces a map on homology $H(C \otimes_R C') \to H(H(C) \otimes_R H(C'))$. Since $H(C), H(C')$ have trivial boundary maps, their tensor product does as well, so $H(H(C) \otimes_R H(C'))$ is simply $H(C) \otimes_R H(C')$. Thus, we have constructed a map $H(C \otimes_R C') \to H(C) \otimes_R H(C')$. And this map splits the short exact sequence which we constructed above.
Application to Topology
The Cross Product in Homology
Just as in the cohomology case, we begin by considering the cross product map \[H_i(X;R) \times H_j(Y;R) \xrightarrow{\times} H_{i+j}(X\times Y;R)\] We will define the cross product in terms of cellular homology. Technically, this means that we must make $X$ and $Y$ CW complexes. However, because of CW approximation, all of our results will apply to general topological spaces. The important insight that lets us define a cross product is the fact that the cellular boundary map on the product space satisfies a signed Leibniz rule $d(e^i \times e^j) = de^i \times e^j + (-1)^i e^i \times de^j$.
First, we prove the result for the cube $I^n$. We give $I$ the cell structure with two vertices and one edge. We will denote the 0-cells of the $i$th copy of $I$ $0_i$ and $1_i$, and we will denote the 1-cell $e_i$. The boundary map is given by $de_i = 1_i - 0_i$. The $n$-cell in $I^n$ is $e_1 \times \cdots \times e_n$, and its boundary is \[d(e_1 \times \cdots \times e_n) = \sum_i (-1)^{i+1} e_1 \times \cdots \times de_i \times \cdots \times e_n\]
Now, write $I^n = I^i \times I^j$ with $i+j= n$. Let $e^i = e_1 \times \cdots \times e_i$ and $e^j = e_{i+1} \times \cdots \times e_n$. Then, our formula tells us that \[d(e^i \times e^j) = de^i \times e^j + (-1)^i e^i \times de^j\] as desired.
To extend this result to the general case, we will use a lemma about the naturality of the cross product.
Let us write $f_*(e^i_\alpha) = \sum_\gamma m_{\alpha \gamma}e^i_\gamma$ and $g_*(e^j_\beta) = \sum_\delta n_{\beta\delta}e^j_\delta$. Then we want to show that $(f \times g)_*(e^i_\alpha \times e^j_\beta) = \sum_{\gamma,\delta} m_{\alpha \gamma} n_{\beta\delta} (e^i_\gamma \times e^j_\delta)$. By the definition of cellular induced maps, the coefficient $m_{\alpha \gamma}$ is the degree of the composition $f_{\alpha \gamma} : S^i \to X^i /X^{i-1} \to Z^i /Z^{i-1} \to S^i$ where the first and last maps are induced by the characteristic maps for the cells $e^i_\alpha$ and $e^i_\gamma$ and the middle map is induced by the cellular map $f$. With the right choice of basepoints in the middle spaces, $f_{\alpha \gamma}$ is basepoint-preserving. The coefficients $n_{\beta\delta}$ are obtained similarly from the composition $g_{\beta\delta} : S^j \to Y^j/Y^{j-1} \to W^j/W^{j-1}\to S^j$.
The coefficients of $e_\gamma^i \times e_\delta^j$ in $(f \times g)_*(e^i_\alpha \times e^j_\beta)$ is given by the degree of the map $(f \times g)_{\alpha\beta, \gamma\delta}:S^{i + j} \to S^{i + j}$. We can obtain $(f\times g)_{\alpha\beta, \gamma\delta}$ by taking the product map $f_{\alpha\gamma} \times g_{\beta\delta}:S^i \times S^j \to S^i \times S^j$ and collapsing the $(i+j-1)$-skeleton of $S^i \times S^j$ to a point.
This means that $(f \times g)_{\alpha\beta, \gamma\delta}$ is the smash product map $f_{\alpha\beta} \wedge g_{\beta\delta}$. So the lemma we want to show boils down to proving that $\deg (f \wedge g) = \deg (f) \deg (g)$ for $f,g$ maps from spheres to themselves.
We can write $f \wedge g$ as $f \wedge \id \circ \id \wedge g$. So we only have to show that $\deg(f \wedge \id) = \deg f$ and $\deg(\id \wedge g) = \deg g$. We will do so by considering the relationship between smash products with spheres and suspension. First, we will consider circles. The smash product $X \times S^1$ can be written $X \times I / (X \times \partial I \cup \{x_0\} \times I)$. This is simply the reduced suspension $\Sigma X$ (recall that $\Sigma X$ is the quotient of the suspension $SX$ which collapses the line $\{x_0\} \times I$ to a point). If $X$ is a CW complex with 0-cell $x_0$, then this quotient $SX \to \Sigma X \cong X \wedge S^1$ just collapses a contractible subspace to a point, so it induces an isomorphism on homology. Now, let $X = S^i$. We have the following commutative diagram
Applying the homology functor to the diagram, we conclude that $Sf$ and $f \wedge \id$ have the same degree. By Proposition 2.33, $Sf$ has the same degree as $f$. So $\deg (f \wedge \id) = \deg f$ (where $\id$ is the identity map $S^1 \to S^1$). Since $S^j$ is the smash product of $j$ copies of $S^1$, we can show by induction that the formula holds when $\id$ is the identity map on $S^j$. The same argument shows that $\deg(\id \wedge g) = \deg g$.
Using this lemma, we can finish proving the proposition. Let $\Phi:I^i \to X^i$ and $\Psi:I^j \to Y^j$ be the characteristic maps of cells $e^i_\alpha \subset X$ and $e^j_\beta \subset Y$ respectively. The restriction of $\Phi$ to $\partial I^i$ is the attaching map for cell $e^i_\alpha$. By the cellular approximation theorem, we can homotope this map to a cellular map. Applying this homotopy does not affect the cellular boundary $de^i_\alpha$ because $de^i_\alpha$ is determined by an induced map on homology groups. So we can assume that $\Phi$ is cellular. By the same argument we can assume that $\Psi$ is cellular. This implies that $\Phi \times \Psi$ is cellular. A cellular map induces a chain map on the cellular chain complexes $C_*(X \times Y)$ and $C_*(Z \times W)$.
Let $e^i$ denote the $i$-cell in $I^i$ and $e^j$ denote the $j$-cell in $I^j$. We have $\Phi_*(e^i) = e^i_\alpha$, $\Psi_*(e^j) = e^j_\beta$, and $(\Phi \times \Psi)_*(e^i \times e^j) = e^i_\alpha \times e^j_\beta$. Therefore, \[d(e^i_\alpha \times e^j_\beta) = d((\Phi \times \Psi)_*(e^i \times e^j))\] Since $(\Phi \times \Psi)_*$ is a chain map, we know that \[d((\Phi \times \Psi)_*(e^i \times e^j)) = (\Phi \times \Psi)_* d(e^i \times e^j)\] We already showed the product rule on the cube $I^{i + j}$ So we know that \[(\Phi \times \Psi)_*d(e^i \times e^j) = (\Phi \times \Psi)_*(de^i \times e^j + (-1)^i e^i \times de^j)\] By our lemma, we can distribute $(\Phi \times \Psi)_*$ over these cross products, so \[(\Phi \times \Psi)_*(de^i \times e^j + (-1)^i e^i \times de^j) = \Phi_*(de^i) \times \Psi_* e^j + (-1)^i \Phi_* e^i + \Psi_*(de^j)\] Using the fact that $\Phi_*$ and $\Psi_*$ are chain maps, we find that \[\Phi_*(de^i) \times \Psi_* e^j + (-1)^i \Phi_* e^i + \Psi_*(de^j) = d\Phi_*e^i \times \Psi_*e^j + (-1)^i \Phi_*e^i \times d\Psi_*e^j\] And by definition, this is just \[de^i_\alpha \times e^j_\beta + (-1)^i e^i_\alpha \times de^j_\beta\] This is precisely what we set out to prove.
The Topological Künneth Formula
For CW complexes $X$ and $Y$, the $n$-cells of $X \times Y$ are products of $i$-cells of $X$ with $j$-cells of $Y$ where $i+j=n$. Thus, $C_n(X \times Y) \cong \bigoplus_{i+j=n} (C_i(X) \otimes C_j(Y))$. This, combined with our formula for the differential above, tell us precisely that $C(X \times Y;R) \cong C(X;R) \otimes_R C(Y;R)$ as chain complexes of $R$-modules. Thus, we can apply the algebraic Künneth formula which we proved above to get a formula for the homology groups of a product space.
Products of CW complexes are problematic because the compactly generated CW topology is not necessarily the same as the product topology. However, both topologies have the same compact sets, so they both have the same singular simplices, which means that they have isomorphic homology groups.
Let $C = C_\bullet(X;R)$ and $C' = C_\bullet(Y;R)$ be the cellular chain complexes with coefficients in $R$. We noted above that $C \otimes_R C' = C_\bullet(X \times Y;R)$. Then the theorem follows from the algebraic Künneth formula. The naturality follows from the naturality guaranteed by the algebraic Künneth formula, combined with the fact that we can homotopy arbitrary maps to cellular maps.


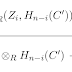



No comments: